استفاده از محاسبات ریاضی در شیمی لازمه حل مسائل استوکیومتری است و یکی از مشکلات اصلی دانش آموزان ، عدم آشنایی و تمرین کافی با برخی از مفاهیم ریاضی و کاربرد آن ها می باشد .مفاهیمی مانند جذر و توان و لگاریتم در ریاضی و به دست آوردن حجم شکل های هندسی مثل کره ، استوانه و حتی هرم و مخروط ، بر خود لازم دانستم که برخی از این مفاهیم را با ذکر مثال از شیمی کنکور مطرح کنم
کاربرد توان در مسائل شیمی : لازم است که چهارعمل اصلی در باره اعداد توان دار را برای حل مسائل مسلط باشیم .
ضرب دو عدد توان دار با پایه های یکسان : ( m و n مخالف صفر ) ،
کابرد ریاضی در شیمی
تقسیم دو عدد توان دار با پایه های یکسان : ، اگر نما یا توان یکسان باشد :
کاربرد ریاضی در شیمی
ضرب دو عدد با نمای یکسان : ،
یا
مثال : ثابت یونش محلول 0.01 مولار هیدروفلوئوریک اسید با pH=4 را حساب کنید .
سوال : آیا جهت تسلط بر محاسبات ریاضی در شیمی لازم است کتاب خاصی را مطالعه کنیم : خیر؛ گاها برخورد می کنم به دانش آموزی که سوال می کنه که آقا من یک کتاب 100 صفحه ای و یا چهار حلقه دی وی دی برای محاسبات ریاضی در شیمی مطالعه کرده ام ، در حالی که باید بداند که اکثرمحاسبات صورت و مخرج کسر ، ضریبی از یکدیگر بوده و به راحتی ساده می شوند .
کاربرد حل معادلات درجه دوم در مسائل شیمی : معادلات درجه دوم که به صورت کلی : نمایش داده می شوند ، که در آن a مخالف صفر است . در جریان حل تست های کنکور شیمی اسید و باز ( فصل اول شیمی دوازدهم ) و یا تعادلات شیمیایی در فصل چهارم شیمی دوازده ناگزیر از حل معادله درجه دوم هستیم تا جواب تست را بیابیم که این جواب اغلب نشان دهنده مقدار یک ماده است .
سوال : منظور از معادله درجه دوم ناقص چیست ؟ معادله درجه دوم که در آن مقدار b و یا C برابر صفر است .
اگر C=0 باشد ، داریم که :
و اگر b=0 داریم که : و a و c هم علامت نباشند می توان گفت که :
روش دلتا : که در آن مقدار دلتا ( مبین معادله) برابر است با :
، اگر مقدار دلتا بیشتر از صفر یاشد ، یعنی معادله دارای دو جواب حقیقی و مجزا خواهد بود . و اگر دلتا برابرصفرباشد ، فقط یک جواب یا ریشه مضاعف دارد . اگر دلتا منفی باشد ، در سطح متوسطه بیان می کنیم که ریشه ندارد و یکی از روش های مهم در حل این نوع معادلات روش تجزیه است . که در این روش سه جمله ای درجه دوم را به حاصل ضرب دو پرانتز تجزیه کرده و هر کدام را مساوی صفر قرار می دهیم . به دست آوردن x در حالت کلی :
نکته : اگر باشد ، آنگاه یکی از ریشه ها برابر 1+و دیگری برابر
خواهد بود .
نکته : اگر باشد ، آنگاه یکی از ریشه ها برابر 1- و دیگری برابر
خواهد بود .
نکته : اگر باشد ، آنگاه ریشه های معادله درجه دوم معکوس هم خواهد بود .
نکته : اگر باشد معادله دارای دو جواب معکوس و قریته هم خواهد بود .
مثال : pH محلول 0.2 مولار اسید ضعیف HA که آن برابر 1 است ، کدام است ؟ ( تجربی کنکور 91 )
همان طور که ملاحظه می کنید در حل این تست شیمی از این تکنیک که حاصل ضرب دوریشه برابر 0.02 – و حاصل جمع دوریشه مجهول برابر 0.1 است استفاده کردیم .
کاربرد لگاریتم در شیمی : لازم است که لگاریتم اعداد 1 ، 2 ، 3 ، 10 و 7 را مسلط باشیم به این طریق می توانیم لگاریتم بقیه اعداد را از حاصل ضرب این اعداد استخراج کنیم .
سوال : لگاریتم 35 برابر چه عددی است ؟
سوال : لگاریتم 6.4 برابر چه عددی است ؟
نکته :
نکته :
سوال : جذر تقریبی 15 کدام است ؟
سوال : جذر تقریبی 1000 کدام است ؟ ( شیمی تجربی 97 )
محاسبه حجم اشکال هندسی در ریاضی و کاربرد آن در تست های شیمی کنکور
حجم کره : ، حجم استوانه :
، حجم مکعب :
حجم مکعب مستطیل : ، حجم محروط :
، حجم هرم :
حجم هرم درواقع : یک سوم حاصل ضرب مساحت قاعده در ارتفاع آن می باشد .
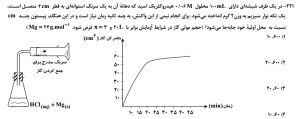
همان طور که ملاحظه می کنید در این سوال ، دانش آموز علاوه بر چالش مفاهیم شیمی با مفهوم نحوه محاسبه حجم استوانه درگیر است ، پس تاکید من بر این است که حتما نحوه محاسبه حجم اشکال هندسی را مسلط شوید .
حل تست : این سوال واکنش بین اسید و منیزیم است که مقدار اسید محدود کننده واکنش بوده در حالی که مقدار منیزیم اضافی است .
پس مقدار گاز آزاد شده از روی مقدار اسید حساب میشه
که اگر صورت و محرج تناسب را پرکنیم
که با توجه به نمودار این حجم گاز در 10 دقیقه یا 600 ثانیه آزاد می شود . و اما این حجم گاز چند سانتی متر پیستون را به عقب می راند یعنی این که با در دست داشتن حجم استوانه می توان ارتفاع آن را حساب کرد . می دانیم که حجم استوانه :
از دید من در این سوال مهم این بود که دانش آموز بر نحوه محاسبه حجم استوانه مسلط باشد تا استوکیومتری ساده این سوال .