جدا شدن الکترون از اتم ( یعنی خارج شدن آن از میدان جاذبه الکتروستاتیکی هستۀ اتم ) را اصطلاحاً یونیزاسیون ( یونش )آن اتم ( یعنی تبدیل به یون مثبت ) می نامند .در این رویداد ، اتم خنثای X در یک نیم واکنش اکسایش( اکسیداسیون ) شرکت می کند و به یون گازی \( X^{+} \)تبدیل می شود . \( X(g)\longrightarrow X^{+}(g)+e^{-} \)
انرژی یونیزاسیون اتم : حداقل مقدار انرژی که باید به اتم خنثای گازی ( در حالت پایه ) داده شود تا یکی از سست ترین الکترون های آن جدا شده ، به یون مثبت گازی ( در همان حالت پایه ) تبدیل شود ، انرژی یونش آن اتم نامیده می شود . در حقیقت این مقدار انرژی ، برای ارتقای الکترون از ترازی که در حالت پایه اتم قرار دارد به تراز بی نهایت \( (n=\infty ) \)مصرف می شود . این مقدار انرژی برحسب الکترون ولت (ev) بر اتم بیان شده و با علائم I ، IE و یا \( \Delta H _{IE} \)نشان داده می شود . ولی معمولاً انرژی یونش را بر حسب کیلوژول بر مول ( و یا کیلوکالری بر مول ) بیان می کنند . البته در این صورت ، برابر انرژی لازم برای تبدیل یک مول اتم گازی در حالت پایه به یک مول یون مثبت گازی در همان حالت است .
در مورد اتم های چند الکترونی ، امکان جداشدن متوالی همه یا تعدادی از الکترون های اتم امکان پذیر است . از این رو ، یونش های متوالی اتم ها نیز باید درنظر گرفت . بدیهی است که با خارج شدن هر الکترون از اتم ، بار موثر هسته و در نتیجه ، نیروی جاذبۀ بین هسته و الکترون های باقی مانده افزایش می یابد . از این رو مقدار انرژی لازم برای یونش های بعدی به ترتیب بیشتر می شود .
گاهی به جای انرژی یونش ، اصطلاح پتانسیل یونش را به کار می برند که بر حسب ولت بیان می شود و آن را حداقل پتانسیل لازم برای جدا کردن یکی از سست ترین الکترون های اتم خنثای گازی در حالت پایه و تبدیل آن به یون مثبت گازی در همان حالت می دانند . مثلاً پتانسیل یونش اتم هیدروژن را می توان برابر 13.6 ولت در نظر گرفت .
روش ترمودینامیکی برای اندازه گیری انرژی یونش : این روش برقانون هس(Hess) مبتنی بوده و در آن از چرخۀ بورن- هابر استفاده می شود . به عنوان مثال اگر بخواهیم انرژی یونش پتاسیم را به روش چرخۀ بورن -هابر حساب کنیم .
ابتدا باید « چرخه بورن- هابر » را در مورد مراحل مختلف فرایند تشکیل بلور یک پتاسیم هالید مثلا پتاسیم برمید مطابق طرح زیر نوشت و با در دست داشتن سایر مقادیر انرژی ( که از طریق اندازه گیری های ترمودینامیکی معین می شوند . ) و با استفاده از رابطۀ موجود بین مقادیر این انرژی ها ، مقدار انرژی یونش پتاسیم را به دست می آوریم .
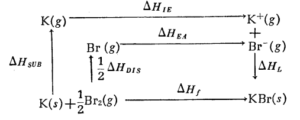
بر اساس قانون هس داریم : \( \Delta H_{f}=\Delta H_{sub}+\frac{1}{2}\Delta H_{Dis}+\Delta H_{L}+\Delta H_{EA}+\Delta H_{IE} \)
\( \Delta H_{sub} \) ( انرژی لازم برای تبدیل پتاسیم جامد به بخار پتاسیم ) برابر 89.1 کیلوژول بر مول
\( \Delta H_{f} \) ( انرژی آزاد شده ضمن تشکیل بلور پتاسیم برمید از پتاسیم جامد و برم مایع ) برابر 392.2- کیلوژول بر مول
\( \Delta H_{Dis} \) ( انرژی لازم برای تفکیک اتمی مولکول برم ) برابر 111.9 + کیلوژول بر مول
\( \Delta H_{L} \) ( انرژی آزاد شده ضمن تشکیل بلور پتاسیم برمید از یون های گازی \( K^{+} \)و \( Br^{-} \) )برابر 687.8 – کیلوژول بر مول
\( \Delta H_{EA} \) ( انرژی الکترون خواهی اتم بُرم ) برابر 324.4- کیلوژول بر مول
\( \Delta H_{IE} \) ( انرژی یونش ( یونیزاسیون ) پتاسیم که باید محاسبه شود . ) با قرار دادن مقدار هریک از این انرژی ها در فرمول هابر ، مقدار انرژی یونش پتاسیم را که برابر 475.8 کیلوژول ( معادل 113.8 کیلوکالری ) بر مول به دست می آید .
\( -392.2=(+89.1)+(\frac{+111.9}{2})+(-687.6)+(-324.4)+\Delta H_{IE} \)
روش طیف نمایی برای اندازه گیری انرژی یونش : بررسی طیف اتم هیدروژن ( و طیف اتم های دیگر در حالت گازی ) نشان می دهد که در سمت طول موج های کوتاهتر ، خطوط طیفی تا حدّی به یکدیگر نزدیک می شوند که از یکدیگر قابل تشخیص نیستند . به بیان دیگر ، طیف اتم به صورت پیوسته در می آید . این رویداد نشان می دهد که انرژی الکترون تا حد معینی افزایش یافته ، از قید جاذبه هسته اتم خارج می شود و تغییرات انرژی آن ، دیگر از محدودیت کووانتومی پیروی نمی کند . این مقدار انرژی در حقیقت همان انرژی یونیزاسیون (یونش ) اتم است . از این رو اگر طول موج آخرین خط طیفی قابل تشخیص ( مرز بین قسمت خطّی و قسمت پیوسته طیف ) در طیف اتم به کمک طیف نما ، مشخص شود ، از روی آن می توان انرژی لازم برای تشکیل چنین خط طیفی که در حقیقت همان انرژی یونش اتم است را به دست آورد .
مثال : انرژی یونش اتم هیدروژن را به روش طیف نمایی حساب کنید .
در مورد اتم هیدروژن ، آخرین خط طیفی به طور تقریب بر طول موج 912 آنگستروم منطبق است . بر اساس روابط موجود بین مقادیر انرژی فوتون تابش های الکترومغناطیسی و فرکانس و یا طول موج این تابش ها یعنی :
\( E=h\nu=\frac{hc}{\lambda} \)خواهیم داشت : \( IE=\frac{hc}{\lambda}= \frac{6.63\times10^{-34}Js\times2.9979\times10^{10}cm/s}{912\times10^{-8}cm}=2.18\times10^{-18}J\\ 2.18\times10^{-18}J\times\frac{1 ev}{1.602\times10^{-19}J}=13.6ev \)
البته همین نتیجه را با استفاده از مدل اتمی بوهر بر اساس معادله زیر می توان به دست آورد .
\( \nu = 3.29\times 10^{15}Hz(\frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}}) \)
زیرا اگر در این رابطه ، ( حالت پایه اتم هیدروژن ) و ( آخرین ترازی که در واقع مرز رهایی الکترون از قید جاذبه هسته است . ) در نظر گرفته شود می توان نوشت :
\( \nu = 3.29\times 10^{15}Hz(\frac{1}{1^{2}}-\frac{1}{\infty ^{2}})=3.29\times10^{15}Hz\\ IE=h\nu=6.63\times10^{-34}Js\times3.29\times10^{15}s^{-1}=2.18\times10^{-18}J\\ 2.18\times10^{-18}J\times \frac{1}{1.602\times10^{-19}J}=13.6 ev \)
ارتباط انرژی یونش اتم با بار موثر هستۀ آن : با توجه به این که برای جدا کردن الکترون از اتم ، باید جاذبۀ الکتروستاتیکی بین آن الکترون و هستۀ اتم را خنثی کرد . از این رو می توان نتیجه گرفت که انرژی یونش ( یونیزاسیون ) اتم از لحاظ قدر مطلق باید با انرژی اتّصال الکترون- هسته (E) برابر باشد . یعنی باید داشته باشیم : \( IE\simeq -E \)
از این رو بر اساس نظریه اتمی بوهر داریم : \( IE=\frac{2K\pi^{2}me^{4}Z^{*2}}{h^{2}n^{2}} \)اگر \( \frac{2K\pi^{2}me^{4}}{h^{2}} \)را که مقدار ثابتی است با A نشان دهیم ، در مورد اتم های چند الکترونی می توان نوشت : \( IE\simeq A(\frac{Z^{*}}{n})^{2}=13.59ev\times(\frac{Z^{*}}{n-\sigma})^{2} \)که در آن \( \sigma \)افت کووانتوم و \( n-\sigma \)عدد کووانتومی موثّر نامیده می شود . هرگاه عدد کووانتومی n برابر 1 ، 2 و یا 3 باشد ، \( \sigma=0 \)است ولی اگر n برابر 4 ، 5 و یا 6 باشد ، \( \sigma \)به ترتیب برابر 0.3 ، 1 و 1.8 است .
مثال : در صورتی که بار موثر هستۀ لیتیم برای الکترون ظرفیت آن برابر 1.27 باشد ، انرژی اولین یونش اتم لیتیم را بر حسب الکترون ولت حساب کنید .
\( IE=13.59ev\times(\frac{Z^{*}}{n})^{2}=13.59ev\times(\frac{1.27}{2})^{2}=5.48ev \)
(یاد آوری این نکته لازم است که مقدار تجربی انرژی اولین یونش اتم لیتیُم برابر 5.39 الکترون ولت است . )
این رابطه نشان می دهد که انرژی یونش اتم ها اصولاً به دو عامل بستگی دارد که عبارتند از:
1- بار موثر هستۀ اتم\( (Z^{*}) \) که هر چه مقدار آن بیشتر باشد ، انرژی یونش اتم نیز بیشتر خواهد بود .
2- فاصله الکترن مورد نظر از هسته که به عدد کووانتومی اصلی (n) یا شماره تراز اصلی انرژی که الکترون مورد نظر در آن قرار دارد ، مربوط است . به طوری که هرچه این فاصله بیشتر (n بزرگتر ) باشد ، انرژی یونش اتم مقدار کمتری خواهد داشت .





برای نوشتن دیدگاه باید وارد بشوید.