طیف ( طیف خطی ) ، معمولاً به مجموعه ای از نوارهای تکرنگ گفته می شود که به صورت نوارهای پهن یا باریک و یا خطوط نسبت به هم دور و یا نزدیک ، پس از عبور تابش الکترومغناطیسی ( نور ) از یک منشور و یا در یک طیف نما قابل مشاهده و عکسبرداری است . نوار طیفی هر جسم از ویژگی های بنیادی و وسیله ای دقیق برای بررسی و شناخت ساختار آن است . اصولاً کشف نوار طیفی عناصر و بررسی آنها یکی از عوامل موثّر در شناخت اتم و پیدایش نظریّه های اتمی جدید بوده است . بر همین اساس است که به عنوان پیش نیازی جهت آشنا شدن با چگونگی کشف ساختار اتم ، طیف ها به ویژه طیف نشری اتم هیدروژن را مورد بررسی قرار می دهیم .
انواع طیف:
الف ) طیف نشری که از طریق برانگیختن اتم ( و یا مولکول ) به وجود می آید و با تابانیدن مستقیم پرتوهای حاصل به طیف نما تشکیل می شود . این نوع طیف را به روش های متفاوتی می توان به دست آورد . مهم ترین این روش ها عبارتند از :
1- قرار دادن جسم در شعله ( طیف شعله ) که در مورد نمک ها متداول است .
2- ایجاد تخلیه الکتریکی درون گازها ( طیف تخلیه ) که در مورد مواد گازی شکل مرسوم است .
3- افزایش دمای جسم جامد تا مرحله التهاب ، که در مورد فلزات و مواد جامد متداول است . ( طیف جسم ملتهب )
4- قرار دادن جسم در گرمای حاصل از یک کمان الکتریکی که در مورد قلزات قلیایی و قلیایی خاکی و ترکیب های آن مرسوم است . ( طیف کمان یا طیف جرقّه )
ب ) طیف جذبی : که پس از عبور از عبور یک تابش معیّن از یک محیط ( جامد ، مایع یا گاز ) و وارد شدن آن در یک طیف نما تشکیل می شود . در چنین طیفی برخی از طول موج های تابش جذب شده به جای آنها در طیف ، نوارها یا خطوط سیاه مشاهده می شود . با توجّه به این بر اساس قانون کرشهُف هر محیط همان تابش هایی را جذب می کند که خود در شرایط مناسب می توانست آنها را تابش کند ، از این رو طیف جذبی هر جسم یکی از ویژگی های آن جسم است و با بررسی آن می توان به ساختار و خواص جسم پی بُرد .
قابل توجّه است که چنانچه به جای طیف نما ، از دستگاه طیف نگار استفاده شود ، مجل طول موج های جذب شده به صورت پیک های جذبی مشخص می شود .
شکل های مختلف طیف
طیف اجسام ، ممکن است به یکی از صورت های زیر تشکیل شود :

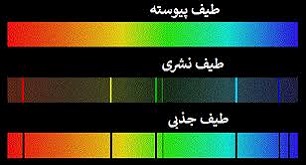
طیف نشری پیوسته که به وسیله جامدات ملتهب ، مایعات و گازهای فوق العاده متراکم در دماهی بالا حاصل می شود . مانند طیف نور سفید که بین رنگ های مختلف آن مرز مشخصی وجود ندارد .
طیف جذبی پیوسته را می توان با عبور نور سفید از یک ماده جامد شفاف ( مثلاً شیشه رنگی ) و یا محلول رنگی به دست آورد .
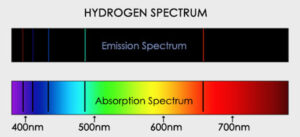
طیف خطّی که نشان دهنده تابش یا جذب مقادیر مشخّص و ناپیوسته ای از انرژی تابشی است و به صورت خطوط طیفی مشخّصی که با قاصله های معینی از یکدیگر متمایزند ، طاهر می شود .
طیف نشری خطّی به وسله اتم ها در حالت گازی در دماهای بالا تابش می شود . مانند طیف نشری خطی اتم هیدروژن در شکل زیر
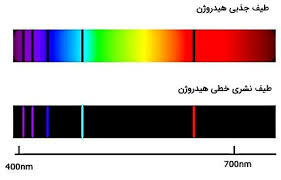
در سال 1883 ، لیوینگ ( Liveing) و دوار(Dewar) دریافته بودند که طیف نشری فلزات قلیایی و قلیایی خاکی ، شامل دسته های متمایزی از خطوط ( سری خطوط طیفی ) است که با نظم مشخّصی به ترتیب طول موج کنار یکدیگر قرار می گیرند . ولی نتوانسته بودند رابطه ای تجربی در باره تعیین محل این خطوط طیفی به دست آورند . طیف نشری اتم هیدروژن نسبتاً ساده تر بود . اولین بار بالمر(Balmer) در سال 1885 طیف نشری اتم هیدروژن را به روش تخلیه الکتریکی به دست آورد و وجود یک سری خطوط طیفی در ناحیه مرئی کسف کرد که به خطوط سری بالمر شهرت یافت . ( شکل زیر )

بالمر با بررسی وضعیت این خطوط ، رابطه ای تجربی برای تعیین طول موج و محل هر یک از آنها در طیف پیشنهاد کرد :\( \lambda=\lambda_{0}\frac{m^{2}}{m^{2}-4} \) که در این زایطه \( \lambda_{0} \)ثابتی است برابر 3646 آنگستروم و m عدد درستی است که می تواند مقادیر 3 ، 4 ، 5 ، 6 و …..و\( \infty \) را اختیار کند . از آنجایی که در روابط مربوط به طیف ، عموماً به جای طول موج ، عکس طول موج یعنی عدد موجی را در نظر می گیرند ، می توان به جای رابطه بالا از رابطه زیر نیز استفاده کرد .
\( \bar{\upsilon}=\frac{1}{\lambda_{0}} .\frac{m^{2-4}}{m^{2}}=\frac{4}{\lambda}(\frac{1}{2^{2}}-\frac{1}{m^{2}}) \) اگر در این رابطه m را برابر 3 ، 4 ، 5 و … قرار دهیم به ترتیب طول موج خطوط طیفی به دست می آید . \( …., H_{\gamma}, H_{\beta}, H_{\alpha} \)سوال : به ازای m=3 کدام خط طیفی از سری بالمر مشخّص می شود ؟
\( \bar{\upsilon}=\frac{4}{3646}(\frac{1}{4}-\frac{1}{9})=1.524\times 10^{-4}A^{-1}\\\lambda=\frac{1}{\nu\bar{}}=6563A \)با توجّه به اندازه آنگستروم به دست آمده ، خط \( H_{\alpha} \)خواهد بود .
ریدبرگ(Rydberg) با بررسی های خود در سال 1890 دریافته بود که رابطه طیفی بالمر جنبه کلّی دارد و آن را برای تعیین طول موج خطوط طیفی سری دیگری که پاشن (Paschen) در ناحیه زیر قرمز طیف نشری اتم هیدروژن کشف کرده بود نیز می توان به کار برد . می توان رابطه بالمر را به صورت کلی زیر نیز ارائه داد :
\( \upsilon\bar{}=R_{H}(\frac{1}{n^{2}}-\frac{1}{m^{2}}) \)که در آن \( R_{H} \)مقدار ثابتی برابر 109677.58 است و به ثابت ریدذبرگ برای اتم هیدروژن موسوم است . n عدد درستی است که در مورد خطوط سری بالمر برابر 2 و برای خطوط سری پاشن برابر 3 و m عدد درست دیگری برابر \( ….,n+4 , n+3 , n+2 , n+1 \)است .
\( m\geqslant n+1 \)بر اساس این رابطه کلی ، چنانچه n برابر 2 و m برابر 3، 4، 5 ، 6 و غیره باشد ، خطوط طیفی سری بالمر مشخّص می شود که در ناحیه مرئی تابش های الکترومغناطیسی قرار دارند . اگر n برابر 3 و m برابر 4، 5 ، 6 ، 7 و غیره باشذ ، خطوط طیفی سری پاشن مشخص می شود که در ناحیه زیر قرمز نزدیک قراردارند . سری های دیگر خطوط طیفی اتم هیدروژن ، پس از کشف ساختار الکترونی اتم ( توسّط بوهر در سال 1913 ) کشف شدند . به طور مثال سری فوند در سال 1924 کشف شد . از آنجایی که می دانیم می توان برای محاسبه فرکانس خطوط طیفی از رابطه :\( \nu=\nu\bar{}.c \)استفاده کرد .
\( \nu=3.3\times 10^{15}(\frac{1}{n^{2}}-\frac{1}{m^{2}}) \)
سوال :طول موج ( بر جسب آنگستروم ) و فرکانس سوّمین خط از سری پاشن را جساب کنید .
برای خطوط طیفی سری پاسن n=3 و برای سومین خط این سری m=6 است ، پس خواهیم داشت : \( \bar{\upsilon}=109677cm^{-1}(\frac{1}{9}-\frac{1}{36})=9140cm^{-1} \)
\( \lambda=\frac{1}{\bar{\nu}}=\frac{1}{9140cm^{-1}}=0.0001094cm\times \frac{1\times10^{8}A}{1cm}=1.094\times10^{4}A \)
\( \nu=3.291\times 10^{15}(\frac{1}{9}-\frac{1}{36})=2.74\times 10^{14}Hz \)




برای نوشتن دیدگاه باید وارد بشوید.